Train Wreck：
给你进出栈的序列，要求为这个序列的每个元素着色，使得每一次入栈操作发生后的栈内序列是两两不同的。
前言：
比赛时就知道括号化序列，但没啥想法，感觉情况太复杂了，后面看题解，发现括号化序列原来可以建树，建树就明了了，建树后就是个贪心，这个套路可以记一下。
思路：
我们可以哪括号化序列转化成树，然后在树上考虑问题，我们很容易观察出，要使满足题意，每个节点的儿子节点必然是没有颜色相同的点。那么如何染色使其实现了
其实我们可以贪心，对于一个节点，要染色其儿子节点，我们最好拿依次拿数量最多的颜色来染色，这样保证最优，如果实现不了则不存在。
代码：
void dfs(int p){
if(ok) return;
if(G[p].size()>q.size()){
ok=1;
return;
}
vector <pll> t;
for(auto v:G[p]){
auto it=q.top();q.pop();
Ans[v]=it.se;
if(it.fi>1) t.push_back(pll(it.fi-1,it.se));
}
for(auto v:t) q.push(v);
for(auto v:G[p]){
dfs(v);
}
}
int main(){
scanf("%d %s",&n,s+1);
m=strlen(s+1);
for(int i=1;i<=n;i++) scanf("%d",&a[i]),c[a[i]]++;
int idx=0;
st.push(0);
for(int i=1;i<=m;i++){
if(s[i]=='('){
G[st.top()].push_back(++idx);
st.push(idx);
}else{
st.pop();
}
}
for(int i=1;i<=n;i++){
if(c[i]) q.push(pll(c[i],i));
}
dfs(0);
if(ok) puts("NO");
else{
puts("YES");
for(int i=1;i<=n;i++) printf("%d ",Ans[i]);
puts("");
}
}OR
给出b，c数组的2–n位置上的数据,构造a数组使得：$(2\le i\le n)b_i=a_{i-1}\ or\ a_i,c_i=a_{i-1}+a_i$ 成立
问可以构造几个满足条件的a数组。
前言：这题比赛想枚举a_1,就能check合法性，但$a_1$太多了，而且check不合理，对于拆二进制，存在加法存在进位不好拆位，没想到还用个公式能将加法和按位与练习起来。
思路:对于$c_i=a_{i-1}+a_i$，转化$c_i=a_{i-1}|a_i+a_{i-1}\&a_i$,即$c_i=a_{i-1}\&a_i$
对于$c_i=a_{i-1}\&a_i$和$b_i=a_{i-1}| a_i$，二进制之间每位都是独立的，我们想到二进制拆位算贡献，对于$a_1$的第$i$位为0或1两种情况，上述两个式子能将$a_2$的第$i$为限制为要么为$0$，要么为$1$，要么没有,可以线性推出。这样算出$a_1$第$i$位可能的答案，然后相乘即可。
代码
int check(int j,int p){
for(int i=1;i<n;i++){
int ch1=b[i]>>j&1,ch2=c[i]>>j&1;
int t1=-1,t2=-1,ok1=1,ok2=1;
if(ch1==1&&p==1) t1=1,t2=0;
else if(ch1==1&&p==0) t1=1;
else if(ch1==0&&p==1) return 0;
else t1=0;
if(t1!=-1&&((p&t1)==ch2)) p=t1,ok1=0;
if(t2!=-1&&((p&t2)==ch2)) p=t2,ok2=0;
if(ok1&&ok2) return 0;
}
return 1;
}
int main(){
cin>>n;
for(int i=1;i<n;i++){
cin>>b[i];
}
for(int i=1;i<n;i++){
cin>>c[i];
c[i]=c[i]-b[i];
}
ll res=1;
for(int i=0;i<=31;i++){
int mul=check(i,0)+check(i,1);
res=res*mul;
}
cout<<res<<"\n";
}Hamburger Steak
题意：
给定$n$ 块牛排及它们分别需要烹饪的时间 $ti$ 和 $m$ 个锅，每块牛排最多只能在两个锅上烹饪，且一个锅不能同时烹饪两块牛排，一块牛排也不能同时在两个锅上烹饪，求所有牛排煮熟所需要的最小时间。
前言：这题一开始我看有两个锅子就猜到时间是平均值，被队友hack这样会有用三个锅子的牛排，后面越想越歪，甚至说这不是多重背包，这复杂度怎么解，比赛快结束也想到锅子的下届的牛排时间最大值，但一直没和我之前想法联系起来，没想到这样就不存在被hack的情况了。。。
思路：
我们很容易知道，烹饪牛排的时间取决于烹饪时间最长的锅，我们可以二分一个锅子的时间，然后check，但是发现check不就是多背包，但背包容量很大，写不了。
我们观察题意又发现，一个牛排能在两个锅子里面，这时发现其实类似于你超出背包的可以并到下个背包，所以把牛排时间之和的平均值$ave=sum/n$，就是锅子时间了，但这时我们发现可能会有牛排要用三个锅子，为什么会用三个锅子呢？因为有块牛排是时间大于$ave$锅子的时间了，其实仔细想想牛排最大时间mx，就是每个锅子的下届，因为不可能每个锅子的烹饪时间比mx还小，这样就保证了不会出现用三个锅子,也保证了不会有同一块牛排同时在两个锅（想想为什么？）的情况了。
代码：
void solve(){
cin>>n>>m;
ll mx=0,sum=0;
for(int i=1;i<=n;i++){
cin>>t[i];
sum=sum+t[i];
mx=max(mx,t[i]);
}
ll T=max(mx,sum/m+(sum%m!=0));
ll tim=0,idx=1;
for(int i=1;i<=n;i++){
if(tim+t[i]<=T){
ll l=tim,r=tim+t[i];
Ans.push_back({1,idx,l,r,0,0,0});
tim=tim+t[i];
if(tim==T) tim=0,idx++;
}else{
ll l1=tim,r1=T;
ll l2=0,r2=tim+t[i]-T;
Ans.push_back({2,idx+1,l2,r2,idx,l1,r1});
tim=tim+t[i]-T;
idx++;
}
}
for(int i=0;i<Ans.size();i++){
if(Ans[i].k==1){
cout<<Ans[i].k<<" "<<Ans[i].id1<<" "<<Ans[i].l1<<" "<<Ans[i].r1<<"\n";
}else{
cout<<Ans[i].k<<" "<<Ans[i].id1<<" "<<Ans[i].l1<<" "<<Ans[i].r1<<" ";
cout<<Ans[i].id2<<" "<<Ans[i].l2<<" "<<Ans[i].r2<<"\n";
}
}
}Counting Triangles
题意
给你一张图，n个点，任何两个点之间都有边，边权要么是0要么是1，问三条边权相等的三角形的数量。
前言：这题比赛时想的离谱，想到都是暴力优化，根本想不到从反面想，没想到反面确实好求。
思路：
这题好像是原题,主要要从反面想，前其实感觉这题关键的是想不到要往反面计数，感觉题目暗示的也不是很明显感觉，但反面就很简单了。
反面求的化就是求颜色不同的三角形，对于一个点，我们只需两个点不同的边乘积，就是颜色不同的边，至于为什么正面难求，因为证明你枚举两个相同的边还需要$check$第三条边是否颜色相同，复杂度过不去
代码：
void solve(){
ll n, seed;
cin >>n>> seed;
srand((int)seed);
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++){
edge[j][i] = edge[i][j] = read();
if(edge[i][j]==0){
ve[i].push_back(j);
ve[j].push_back(i);
}
}
ll ans=0;
for (int i = 0; i < n; i++)
ans += (n - 1 - ve[i].size())*ve[i].size();
ans /= 2;
cout << (n*(n - 1)*(n - 2)) / 6 - ans << endl;
return 0;
}Black and white
题意：
给你一个 $n\times m $的矩形，每填一个格子都有一个花费，当你把一个矩形四个角中任意三个角填上了，另外一个角自动填上，问你最小花费是多少
前言： 这题比赛完全没啥想法，代码都没码，事实上这转化确实也离谱，一般都想不到，既然做到了就记录一下。
思路：
这题转化比较离谱，如果没见过一样的套路，大概怎么想都想不到。
我们可以在本子上画可以看出，大概我们在横则一条，竖则一条就能满足条件。
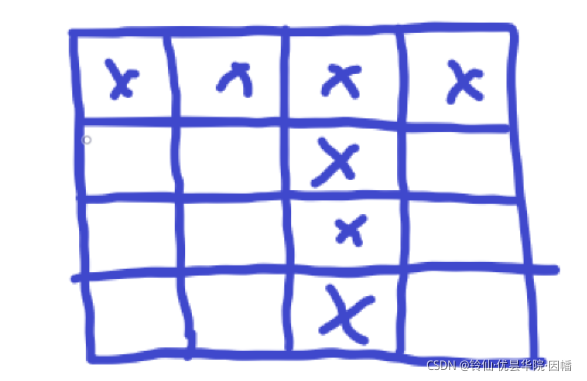
这样也可以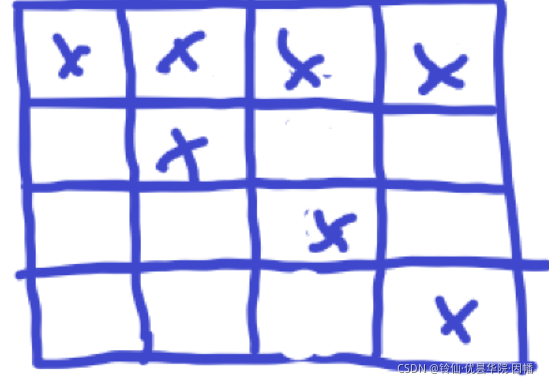
我们发现只要把行和列抽象成点，保证连通就行，这样就是个最小生成树（离谱）
代码：
void init(){
for(int i=1;i<=n+m;i++){
f[i]=i;
}
}
int fin(int x){return f[x]==x? x:f[x]=fin(f[x]);}
int bing(int x,int y){
int f1=fin(x),f2=fin(y);
if(f1==f2) return 0;
f[f2]=f1;
return 1;
}
int main(){
cin>>n>>m>>a>>b>>c>>d>>p;
init();
ll x=a;
for(int i=1;i<=n*m;i++){
x=(((x*x%p)*b%p)+x*c%p+d)%p;
ho[x].push_back(pll((i-1)/m+1,(i-1)%m+1+n));
}
ll cnt=0,ans=0,ok=1;
for(int i=0;i<p&&ok;i++){
for(int j=0;j<ho[i].size()&&ok;j++){
if(bing(ho[i][j].fi,ho[i][j].se)){
cnt++;
ans+=i;
}
if(cnt==m+n-1){
ok=0;
break;
}
}
}
cout<<ans<<"\n";
}Stack
题意:
单调栈中先放数，然后计算出栈的大小存入b数组。现在给你b的部分数组，然后让你还原出一种a数组。
前言： 比赛时发现构造$b_i$数组，和不合法的情况，但和队友口胡了一个很离谱的做法，最后做法假了，一堆bug，而且用到线段树码量也离谱，以后反思下这种码量离谱的做法正确性还是要慎重再慎重，多从题目本质验证做法，不要太凭感觉。
思路： 首先$b$数组上升肯定只能一个一个上升，由这个我们很容易构造出$b$数组。然后我们相同的$b_i$数组中数字相同说明，在当前位置出栈到与上个$b_j$一样的位置，所以我们$b$数组相的数组同我们构造从后往前连续的排列即可。
代码：
#include <iostream>
#include <vector>
using namespace std;
const int N=1e6+7;
int n,m,ans[N],b[N];
vector <int> ho[N];
int main(){
scanf("%d %d",&n,&m);
for(int i=1,x,v;i<=m;i++) scanf("%d %d",&x,&v),b[x]=v;
int idx=0;
for(int i=1;i<=n;i++){
if(!b[i]) b[i]=++idx;
else if(b[i]-idx>1) return puts("-1"),0;
else idx=b[i];
ho[b[i]].push_back(i);
}
int cnt=0;
for(int i=1;i<=n;i++){
while(ho[i].size()){
ans[ho[i].back()]=++cnt;
ho[i].pop_back();
}
}
for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
cout<<"\n";
} 航电思维题
Median
题意：
给定一个长度为 m 的数组 b，现在需要将 $1 - n$ 区间内的 $n$ 个数字分为 $m$ 个集合（可以不连续，但需要满足单调性），并满足第 $i$ 个集合的中间数等于数组$ b $中的第$ i$ 位，问是否可完成该操作。
前言： 这题也凭感觉口胡了个很离谱的做法，最后也假了，看题解发现做法确实妙。
思路：
这题离大谱，直接贴官方题解
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QAV1xjj0-1636033005370)(C:\Users\5\AppData\Roaming\Typora\typora-user-images\image-20211104201819903.png)]](https://img-blog.csdnimg.cn/9968c69de81b422f8fb952c272e8d1c4.png?x-oss-process=image/watermark,type_ZHJvaWRzYW5zZmFsbGJhY2s,shadow_50,text_Q1NETiBA6ZOD5LuZwrfkvJjmmJnljY7pmaLCt-WboOW5oQ==,size_20,color_FFFFFF,t_70,g_se,x_16 "[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QAV1xjj0-1636033005370)(C:\Users\5\AppData\Roaming\Typora\typora-user-images\image-20211104201819903.png)]")
代码
void init(){
ho.clear();
}
void solve(){
cin>>n>>m;
init();
for(int i=1;i<=m;i++){
cin>>a[i];
}
sort(a+1,a+1+m);
a[m+1]=n+1;
for(int i=1;i<=m+1;i++){
ho.push_back(pll(a[i]-a[i-1]-1,i-1));
}
sort(ho.begin(),ho.end());
ll sum=0;
for(int i=0;i<ho.size();i++){
sum=sum+ho[i].fi;
}
sum=sum-ho.back().fi;
ll tem=ho.back().fi-sum;
if(ho.back().se>=tem){
cout<<"YES\n";
}else{
cout<<"NO\n";
}
}Yiwen with Sqc
题意:
给一个字符串，对于每个小写字母ch，问所有区间内ch出现次数的平方和，其中|s|<
因为答案很大，所以对998244353取模（答案很大，忍一下
前言： 这题之前在CF写过一道算贡献和着差不多，但着有平方，不能整体操作，然后我就被困住了，没想到对于带平方的我们能进行类似线段树的区间加减x，然后换种方法算贡献就行了，有时对于一种想法不行，确实不要陷入进去了
思路：
这题如果你算某个字符的答案，你对于其字符标位1，然后算[l,r]的前缀和，其为[l,r]前缀的答案，你要算其所有字串的答案，需要移动向前$l$,当移动到对应字符时，由于前缀的其贡献消失，[l,r]区间要减1，特别的这题算的是平方，平方我们可以把平方开出来，同过维护几个变量，就能对其进行区间减1了。
代码：
void init(){
for(int i=0;i<26;i++) sa[i].clear();
}
ll gao(int p){
ll pw=0,t=0,res=0;
for(int i=0;i<sa[p].size();i++){
if(i+1<sa[p].size()){
ll len=sa[p][i+1]-sa[p][i],id=sa[p][i];
pw=((pw+2*t%mod)%mod+id)%mod;t=(t+id)%mod;
res=(res+pw*len%mod)%mod;
}else{
ll len=n-sa[p][i]+1,id=sa[p][i];
pw=((pw+2*t%mod)%mod+id)%mod;t=(t+id)%mod;
res=(res+pw*len%mod)%mod;
}
}
return res;
}
void solve(){
scanf("%s",a+1);
n=strlen(a+1);
init();
for(int i=1;i<=n;i++){
sa[a[i]-'a'].push_back(i);
}
ll ans=0;
for(int i=0;i<26;i++){
ans=(ans+gao(i))%mod;
}
printf("%lld\n",ans);
}
int main(){
scanf("%d",&T);
while(T--) solve();
}