矩阵
矩阵与向量
向量我们可以看成是一个一行或一列矩阵
矩阵我们可以看成是一行或一列矩阵排成一起
行向量和列向量
假设我们规定一行——即$1 \times m$ 的矩阵为向量,那么称之为行向量
假设我们规定为一列——即$n \times 1$的矩阵为向量,那么称之为 列向量
为什么要区别行列向量呢?
区别了行列向量,我们能规定矩阵与向量相乘时,是左乘向量还是右乘向量。
一般的如果是行向量,那么他就是右乘向量,即
$\vec v^{*} = \vec v * M$
一般的如果是列向量,那么他就是左乘向量,即
$\vec v^{*} = M * \vec v$
细心的也能发现,划分左右向量后,矩阵是横着排列,还是竖着排列也确定了。
矩阵几何解释
一般来说,矩阵能够描述任意的线性变换。
线性变换,简单来说保留了坐标系的网格全部平行,没有扭曲。
矩阵式如何变换向量的
首先提问,在二维空间里面,存在两个线性无关的向量,为$\vec p$、$\vec q$,那么在形如向量$\vec v$:
$v = xp + yq$,存在多少结果,换句话说能表示那些向量。
事实上很容易相当,他能表示出空间中任意一个向量
将这条结论扩张到三维空间中,我们也能得到类似的结论
$\vec v = x\vec p + y\vec q + z\vec r$
我们将这个式子换个方法写下
$$ \begin{pmatrix} v_x \\ v_y \\ v_z \end{pmatrix} \ = \begin{pmatrix} p_x & q_x & r_x\\ p_y & q_y & r_y \\ p_z & q_z & r_z \end{pmatrix} \times \begin{pmatrix} x \\ y \\ z \end{pmatrix} $$
从上面式子我们看出向量$(x\ y \ z)^T$可以左乘,由向量$\vec p \ \vec q \ \vec r$矩阵构成的矩阵,可变换成任意的向量$\vec v$。
矩阵的形式
从上面式子我们可以将向量$\vec p \ \vec q \ \vec r$看做基向量——即矩阵的每一列。我们可以把向量乘以一个矩阵看作进行了一次坐标变换。
下面我们在二维坐标下举例。
看下列$2 \times 2$的矩阵
$$ M = \begin{pmatrix} 2 & -1 \\ 1 & 2 \end{pmatrix} $$
我们拿出基向量
$$ \vec p = (2 \ \ 1)^T \\ \vec q = (-1 \ \ 2)^T $$
在二维坐标系下作图
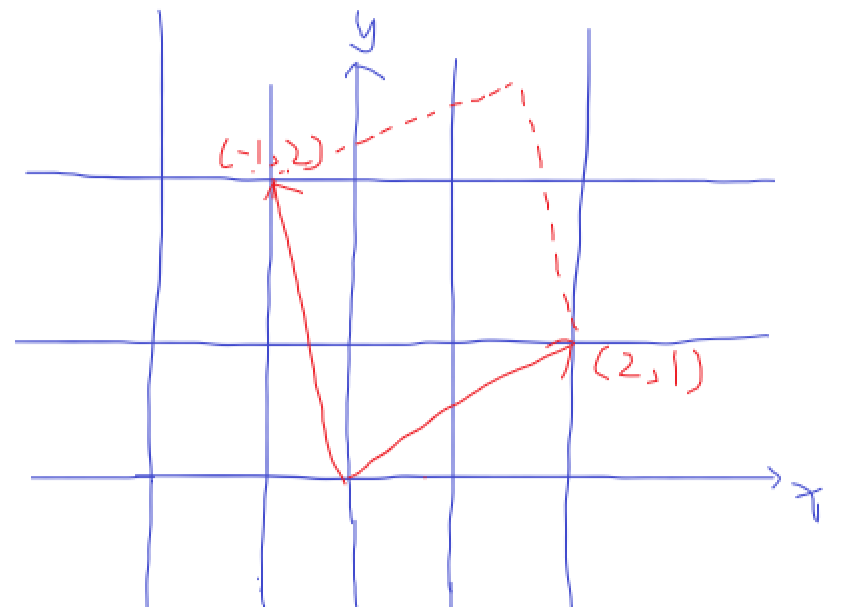
假设坐标系存在个物体
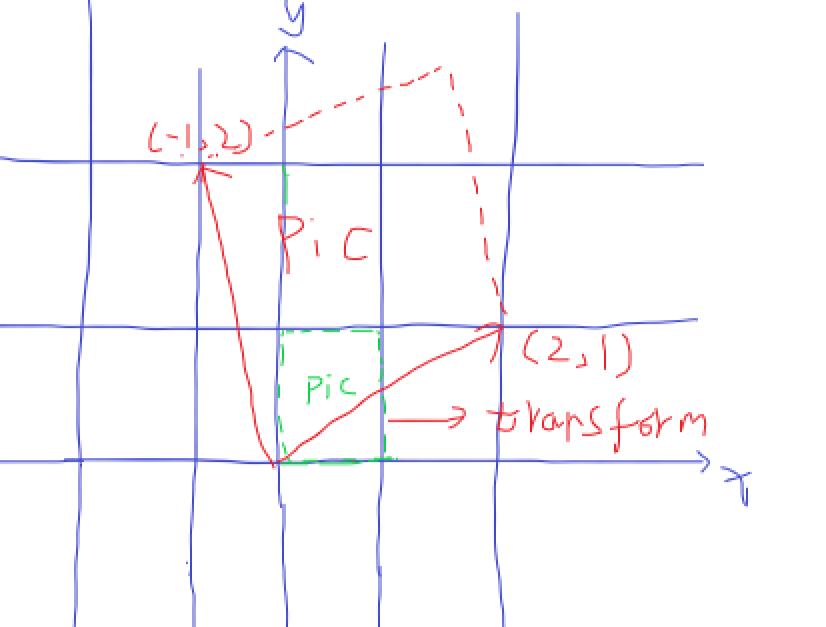
此处评论已关闭