线性变换

物体变换与坐标系变换

简而言之：

• 物体变换 是变换单个物体，相对与我们参考的是世界坐标系
• 坐标系变换类似我们将物体放在原点，局部坐标和世界坐标重合(类比照相机空间)，变换的是其他所有物体

物体变换的变换矩阵与坐标系的变化矩阵互逆

旋转

2D中的旋转

首先咱们还是讨论下二维坐标下旋转,结合下面图片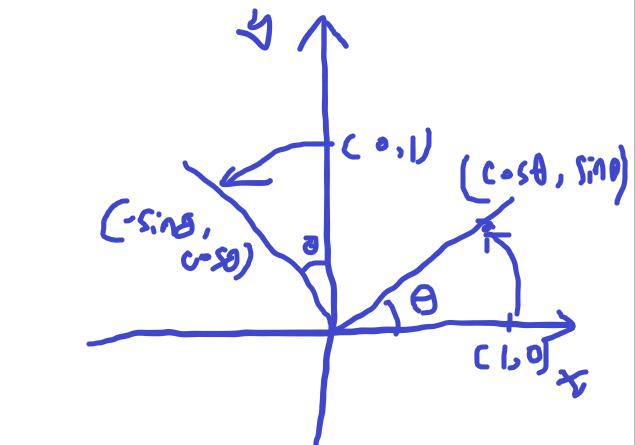

可以得出矩阵

$$ \begin{pmatrix} \cos \theta & -\sin \theta\\ \sin \theta & \cos \theta \end{pmatrix} $$

3D中的旋转

首先申明：三维坐标旋转都是考虑绕过原点的旋转轴旋转的。
在这里我们也必须确立绕轴旋转$\theta$角度时，那个方向被认定为正方向，接下来我们逐步分析

左手坐标和右手坐标

判断左手右手坐标的方式如图，是事实观察就会发现，大多数时候横为x，竖为y，但对于z，有的是朝屏幕内，有的朝屏幕外，这就有了左右手坐标划分。

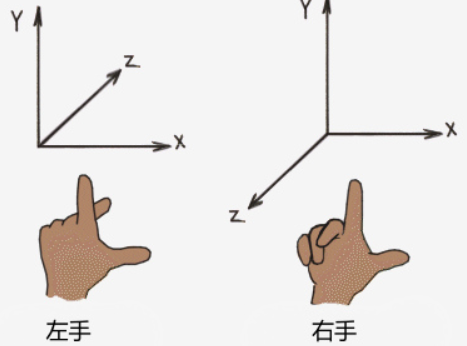
确定了是左手还是右手坐标系，那么我们就能更具一条结论判断旋转的正方向，即：

• 对于左手坐标系，用左手握住旋转轴，拇指朝旋转轴正方向，四指弯曲方向即正方向

• 对于右手坐标系，用右手握住旋转轴，拇指朝旋转轴正方向，四指弯曲方向即正方向

  

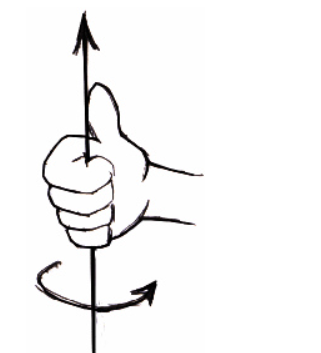
绕3D坐标轴旋转

更多关于3D旋转详细请看欧拉角，也可以看四元数

放缩

我们定义缩放一般以原点为中心缩放物体，我们可以定义k为缩放的比例因子

沿坐标轴的缩放

如果每个轴的缩放因子相同，则是均匀缩放，否则非均匀

我们可以直接凭直觉得出3维空间缩放矩阵

$$ \begin{pmatrix} k_x & 0 & 0 \\ 0 & k_y & 0 \\ 0 & 0 & k_z \\ \end{pmatrix} \\ $$

$$ \text{公式 : 沿坐标缩放} $$

沿任意轴缩放公式

我们可以$\vec n$为平行于缩放方向的单位向量
$k$为该方向的缩放因子
则得出3维坐标缩放矩阵

$$ \begin{pmatrix} 1 + (k - 1) n_x ^2 & (k - 1) n_x n_y & (k - 1) n_x n_z \\ (k - 1) n_x n_y & 1 + (k - 1) n_y^2 & (k - 1) n_y n_z \\ (k - 1) n_x n_z & (k - 1) n_z n_y & 1 + (k - 1) n_z^2 \\ \end{pmatrix} $$

$$ \text{公式 : 沿任意方向缩放} $$

正交投影

投影意味这降维，当某个方向的缩放因子为零的时候，就意味着将其正交投影到垂直于该方向的平面

向坐标平面正交投影

我们很容易得正交投影于坐标面的矩阵

$$ p_{xy} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \\ \end{pmatrix} $$

$$ \text{公式：平行与xy面} $$

$$ p_{xz} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$

$$ \text{公式：平行与xz面} $$

$$ p_{yz} = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} $$

$$ \text{公式：平行与yz面 } $$

任意面的正交投影

由投影等于缩放因子为零，我们推出任意面矩阵

$$ \begin{pmatrix} 1 - n_x^2 & -n_xn_y & -n_xn_z \\ -n_xn_z & 1-n_y^2 & -n_yn_z \\ -n_xn_z & -n_xn_y & 1-n_z^2 \\ \end{pmatrix} $$

$$ \text{公式：投影于n向量垂直的平面} $$

镜像

镜像类似把物体沿直线（2D）或平面（3D）“翻转”过来，也相当于缩放因子为-1时

二维空间

$\vec n$为垂直于翻转翻转轴的向量，那么我们得到矩阵

$$ \begin{pmatrix} 1-2n_x^2 & -2n_xn_y \\ -2n_xn_y & 1-2n_y^2 \\ \end{pmatrix} $$

$$ \text{公式：二维空间翻转} $$

三维空间

$\vec n$为垂直于翻转平面的向量，那个得到矩阵

$$ \begin{pmatrix} 1-2n_x^2 & -2n_xn_y & -2n_xn_z \\ -2n_xn_y & 1-2n_y^2 & -2n_yn_z \\ -2n_xn_z & -2n_xn_y & 1-2n_z^2 \\ \end{pmatrix} $$